Simple Harmonic Motion - A "simple" but ubiquitous concept

From clocks that mark the passage of time, to the metronome that sets pace to our

instruments, objects that perform periodic motion are all around us. It is essential,

therefore, to explore the mechanics of periodic motion and understand the physics and

mathematics that govern various oscillating systems.

Author: Sammith S, Editor: Iris Litiu

1. Article overview

This article explores the most basic form of periodic motion known as simple harmonic

motion(SHM).We will go over the characteristics of simple harmonic oscillators and

study idealized physical systems to derive the equations for the motion of these oscillators.

2. Characteristics of simple harmonic oscillators

A great example for a simple harmonic oscillator is the pendulum which is illustrated

below. Point A is the equilibrium position for the pendulum. When we draw the bob

of the pendulum away from its equilibrium position to point C and release it, we see

that the bob overshoots the equilibrium position and stops momentarily at point B (the

extreme of its motion), before swinging back towards the equilibrium and reaching its

initial position (Point C). In a nutshell, the motion of the pendulum is due to the gravitational force (the restoring force) attracting the bob towards the equilibrium position

and the inertia of motion causing the bob to overshoot and reach the other extreme of

its motion.

Figure 1: A simple harmonic oscillator

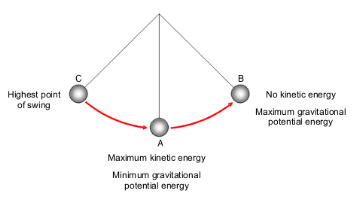
The figure also highlights the breakdown of mechanical energy of the bob. When the

bob is brought to point C where the vertical displacement is the highest, the bob has

maximum gravitational potential energy and no kinetic energy. When it passes through

the equilibrium position, the vertical displacement is zero and the bob has no gravitational potential energy but has maximum kinetic energy. So, the velocity is maximum

at the equilibrium position.

The above physical characteristics of the pendulum are common to all simple

harmonic oscillators:

• Periodic motion

• Restoring force (gravitational force in the case of a pendulum)

• Inertia of motion causing the oscillating particle to overshoot the equilibrium position

• Constant flow between kinetic and potential energy

3. Idealized oscillating systems

We generally utilize idealized physical systems as real physical systems tend to be

complicated and contain a number of factors. We begin with an idealized system and

then add the necessary variables to obtain the best solution to the problem at hand.

3.1 Mass attached to a horizontal spring

The first oscillating system that we consider is a mass attached to a horizontal spring.

Here the force of gravitation is negated by the normal force and hence, there is no

displacement in the y direction. This system is idealized as we assume that the

surface is frictionless and the mass of the spring is negligible.

Figure 2: Mass attached to a horizontal spring

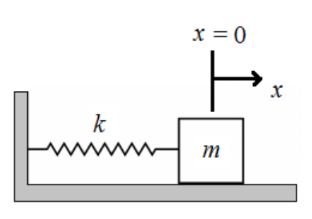
The equilibrium position for this system is where the spring is un-stretched which is

marked as 0.x is defined as the displacement of the mass from the equilibrium

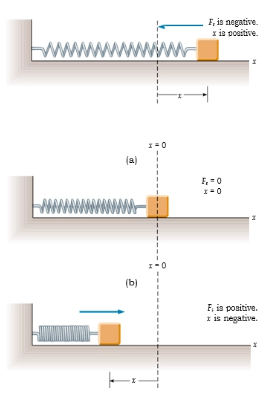
position. When the spring is extended, i.e., is positive, the restoring force acts in the

opposite direction to x to pull the mass back to the equilibrium position. When the

spring is compressed, i.e., x is negative, the restoring force acts in the opposite

direction of x to push the mass back to the equilibrium position.

Figure 3: The direction of the restoring force for displacements in the mass

The force produced by the spring can be described by Hooke’s law. The Hooke’s

law gives us the strength of the restoring force which is proportional to the extension

or compression of the spring (which is x).This can be written as F ∝ x.

The constant of proportionality becomes the spring constant k which is defined as the

force per unit displacement and the equation for the restoring force becomes

The negative sign indicates that the force always acts in the direction opposite to the

displacement. However, this system must obey Newton’s first law of motion which means that

Acceleration is a measure of the rate of change in velocity. Velocity, which is

v(t)=dx/dt, is the rate of change of position with respect to time. So this means that

acceleration is the derivative of a derivative: the second derivative with respect to

position, or the derivative of velocity. Now that we know acceleration is the second

time derivative of position,

By substituting equation 3 in equation 2, we get,

Further simplification lets us write the equation as,

By assuming that,

We can write,

w^2 is basically the restoring force per unit displacement per mass. The usage ofw2

instead of w is to make the calculations simpler and it will become evident as we

explore more of SHM. The equation that we have obtained is the equation of SHM

and all simple harmonic oscillators have an equation of this form.

4.2 Mass on a vertical spring

Another system that we consider is a mass attached to a vertical spring and the

setup is shown below.

Figure 4: Mass attached to a vertical spring

In this system, we have the gravitational force acting on the mass. When you initially

attach the mass to the spring, we see that the length of the spring extends by ∆l.

To find out the resultant force on the mass, we need to subtract the force exerted

upwards by the spring from the gravitational force (we assume that displacements in

the downward direction are positive).Hence, the resultant force on the mass is given

by,

The above equation can also be written as mg = k∆l. The resultant force acting on

the mass is given by F = mg−k(∆l+x) and subsequent expansion of the equation

gives rise to F = mg−k∆l−kx. But we already know that mg = k∆l, which gives

rise to,

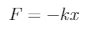
This is identical to the one obtained when we derived the equation of motion for a

mass attached to a horizontal spring.

Now let us try to derive the equations for displacement, velocity and acceleration for a

simple harmonic oscillator. When we plot the motion of any simple harmonic

oscillator, we get a plot that resembles the cosine function.

Figure 5: Periodic motion of a simple harmonic oscillator

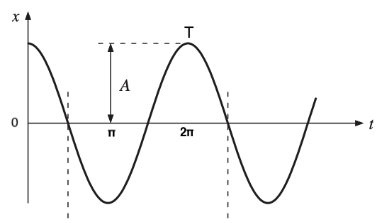
Figure 5 plots the displacement x of the mass with respect to time t. The maximum

displacement of the mass is known as the amplitude (A) and we can see the amplitude

at t=0.The time it takes for the mass to complete one cycle of oscillation is called

period (T). Frequency gives us the number of cycles of oscillations that happen per

unit time and is denoted by v. The relationship between period and frequency is given

by,

The units of frequency are Hertz where 1 Hertz is equivalent to 1 cycle per second.

When we consider figure 5, we see that the 2πt/T is the angle covered from 0 to 2π as t

goes from 0 to T. Hence, we can express displacement as,

Next, we define the angular frequency as,

By substituting equation 11 in equation 10, we get,

It is now simple to obtain the velocity and acceleration. Keeping in mind that,

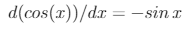
and that,

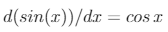
By taking the first time derivative of x, we get velocity as,

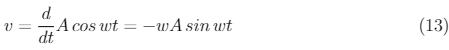
And by taking the second time derivative of x, we obtain the acceleration as,

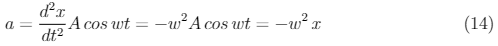
We can see that equation 7 equals equation 11 and the reason for writing w^2, which is

the square of the angular frequency, becomes evident. We have also derived the

equations for displacement, velocity and acceleration when x = A. The graphs for the

derived equations are illustrated below.

Figure 6: Displacement, velocity, and acceleration for a harmonic oscillator

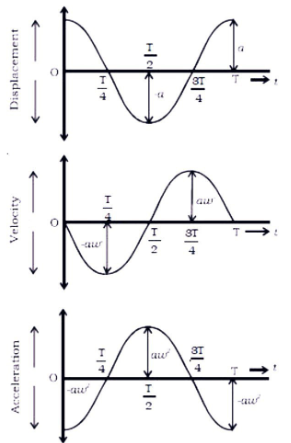
The aligned time axes makes it easier for us to examine figure 6. When x is at the

highest (i.e., at A), we see that the velocity is 0. We also see that the velocity is

maximum when the mass is at its equilibrium position.